什么是LCA?
祖先链
对于一棵树T,若它的根节点是r,对于任意一个树上的节点x,从r走到x的路径是唯一的(显然),那么这条路径上的点都是并且只有这些点是x的祖先。这些点组成的链(或者说路径)就是x的祖先链。
LCA
根据名字来说,最近公共祖先就是两个点最近的相同祖先。实际上也可以理解为:两个点的祖先链深度最大的那个交点。极端的情况下,LCA可以就是两个点之一,或者就是根节点root。
顺便贴下eg:
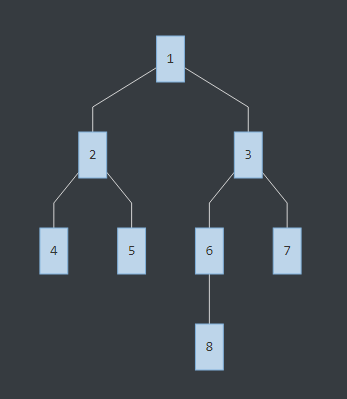
树中节点8和7的LCA为3,节点4和7的LCA为1,节点5和2的LCA为2。
*可以写成LCA(u,v)=w的形式
LCA的求法
问题:给出一棵有n(n≤500000)个节点的树,并给出m(m≤500000)个询问,每个询问给出两个点u,v,请你求出每个u,v的LCA。
1.向上标记法
首先根据定义来。LCA(u,v)是两个点的祖先链的第一个交点(从下往上第一个)。那么我们可以先从u开始往根节点走,那么走到的点都是u的祖先,走出的路径就是u的祖先链。那么我们在走的时候把祖先链上的点都标记一下,再从v开始往根节点走,走到的第一个被标记过的点就是LCA了。最坏的情况下时间复杂度为O(n),总共就是O(n*m)。显然不能满足题目的需要~
2.树上倍增法
一个一个地跳显然太慢,不如加加速?怎么加速呢?根据一贯套路,慢了就倍增~为什么这里不倍增呢?那就倍增一下咯~
树上倍增的思路不同于标记的思路,因为倍增的时候是无法标记的。反正跳得快,就干脆让u,v都跳一跳,跳到同一个点时就到了LCA了。不过不是一上来就一起跳的,树上倍增的预处理可是很浩大的。
首先预处理出倍增之后跳到的点是谁。设f(i,j)为节点i往上跳2^j步到达的节点,那么
f(i,j)=f(f(i,j-1),j-1)
初始化f(i,0)=fa(i),即i的父亲。(刚才那里真的是零......)
设d(i)为i的深度,顺便把这货也处理出来(这么简单就不讲了)。
弄了这么多之后还不能直接两个点倍增。首先需要将深度大的那个点(假设是v)往上倍增到和u深度相同为止。基于二进制转化的思想,任何树都可以用二进制表示出来,所以绝对是可以倍增到同一深度的。
接着,两个点同时倍增。经过若干次倍增之后,若fa(u)==fa(v),那么fa(u)就是LCA了。
放上预处理的代码:
xxxxxxxxxx
inline void bfs(){ q.push(s);
d[s] = 1;
while(!q.empty()){ int u = q.front(); q.pop();
for(int i = head[u]; ~i; i = e[i].next){ int v = e[i].to;
if(d[v]) continue;
d[v] = d[u] + 1,f[v][0] = u;
for(int j = 1; j <= t; j++) f[v][j] = f[f[v][j - 1]][j - 1];
q.push(v);
}
}
}
//在main函数中
t = (int)(log(n) / log(2)) + 1;
bfs();
以及倍增的代码:
xxxxxxxxxx
inline int lca(int &u, int &v){ if(d[u] > d[v]) swap(u, v);
for(int i = t; i >= 0; i--) if(d[f[v][i]] >= d[u]){ v = f[v][i];
}
if(u == v) return u;
for(int i = t; i >= 0; i--) if(f[u][i] != f[v][i]){ u = f[u][i];
v = f[v][i];
}
return f[u][0];
}
*一般数组会开成这样:
xxxxxxxxxx
int f[maxn][20];
这样一般就够用了。
预处理的复杂度为O(nlogn),每个询问的复杂度为O(logn),一共就是O((n+m)logn),可以跑过题目的数据。
3.Tarjan
不同于倍增,Tarjan是一种离线算法,并且很优秀很优秀(就是难写)。考虑到刚接触LCA的OIer可能难以理解Tarjan,这里我用几种不同的方式来讲。
本人的方式:你首先在心里构造出一棵树来......标记祖先链的方式其实可以多个询问一起进行。首先依照Tarjan的流程,遍历这棵树。假设现在遍历到了点u,并且开始回溯,那么你可以想象在回溯的过程中实际上是从节点u往上拉出了一条祖先链。当拉链子拉到了一处分叉,并且分叉的另一边还没去过时,就停止拉链,往下走。假设这个过程中走到了节点v并开始回溯,并且询问里有问u和v的LCA,那么在从v回溯的过程中相当于从v开始也拉上去了一条祖先链,会一直拉到之前的分叉处,此时u和v的祖先链便第一次相交,交于分叉处,这个分叉处便是LCA(u,v)。也就是说,当我们遍历到一个点v,发现询问里有LCA(u,v)这个询问,并且从u已经拉出了祖先链,那么LCA(u,v)就是此时u的祖先链的顶端。其实我们不该只局限于这一个询问,从宏观上看,在遍历的过程中我们其实从每个回溯过的点都拉出了一条祖先链来。如果你觉得拉的链子太多,我们可以剪掉一些:只留下询问里涉及的点的祖先链。那么这些祖先链的交点就是遍历过程中走到的那些分叉口,所以一次遍历就可以求出所有询问的LCA。
还是附个流程图吧......

我们先在要求:LCA(9,10),LCA(9,5),LCA(8,7),LCA(9,8)。
然后我们从左到右遍历下去,遍历到了9号节点,便往回拉祖先链:
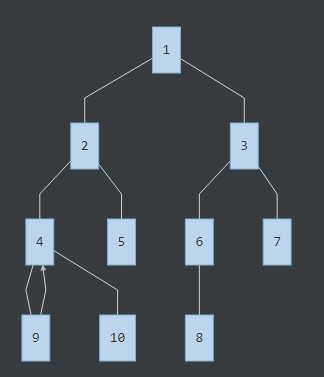
(箭头的边是祖先链)现在拉到了4号节点,发现有分叉,往下走到10号节点,发现询问里有LCA(9,10)这个询问,并且从9已经拉出了祖先链,那么LCA(9,10)就是此时9的祖先链的顶端:4号节点。(由于关于10的询问都处理完了,10的祖先链就不画了)此时继续往上拉链:
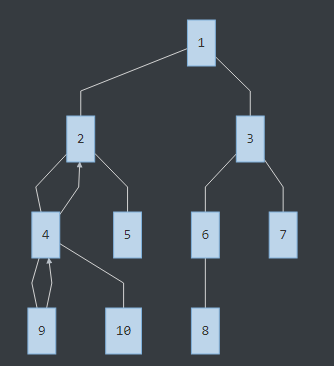
此时发现又有一个分叉,便往分叉走,走到5的位置,并发现询问里有LCA(9,5),那么LCA(9,5)就是此时9的祖先链的顶端:2号节点。(5的祖先链也不画了)继续往上拉链。
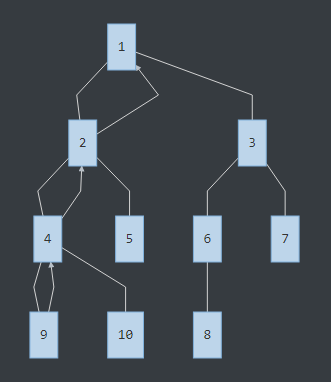
发现有分叉,往下走到8的位置,发现询问里有LCA(9,8),那么LCA(9,8)就是此时9的祖先链的顶端:1号节点。接着从8往上拉祖先链:

发现有分叉,往下走到7的位置,发现询问里有LCA(8,7),那么LCA(8,7)就是此时8的祖先链的顶端:3号节点。
这样应该就可以理解了......整个遍历的复杂度为O(n),加上回答询问的复杂度总共也才O(n+m)。像上面题目里的数据范围可以随便跑。
下面是教练的方式:拉祖先链的过程可以想象成灌水......当你往下灌到底部时,水就会慢慢往上涨,当涨到一个分岔口时就会往另一边流。其实也差不多啦~
附上存询问的代码(用邻接表来存,方便查询):
xxxxxxxxxx
struct edge{ int to, next, lca;
edge(){} edge(register const int &_to, register const int &_next){ to = _to,next = _next;
}
}qe[maxm << 1];
int qhead[maxn], qk;
inline void qadd(register const int &u, register const int &v){ qe[qk] = edge(v, qhead[u]);
qhead[u] = qk++;
}
//main函数中
memset(qhead, -1, sizeof qhead);
for(register int i = 1; i <= m; i++){ scanf("%d%d", &u, &v); qadd(u, v),qadd(v, u);
}
然后是Tarjan函数:
xxxxxxxxxx
inline int find(register const int &x){ if(fa[x] == x) return x;
return fa[x] = find(fa[x]);
}//用并查集的方式查找祖先链的顶端
void LCA_tarjan(int u, int pre){ vis[u] = true;
for(register int i = head[u]; ~i; i = e[i].next){ int v = e[i].to;
if(v != pre){ LCA_tarjan(v, u);
fa[v] = u;//拉祖先链
}
}
for(register int i = qhead[u]; ~i; i = qe[i].next){ v = qe[i].to;
//如果v已经拉出了祖先链,就回答询问
if(vis[v]) qe[i].lca = qe[i ^ 1].lca = find(v);
}
}
//main函数中
for(register int i = 1; i <= n; i++) fa[i] = i;
LCA_tarjan(s, 0);//s为根
以及回答询问:
xxxxxxxxxx
for(int i = 0; i < qk; i += 2) printf("%d\n", qe[i].lca); 考虑到并查集的存在,Tarjan的复杂度其实为:O(n+mlogn),只不过实际远远达不到这个程度而已。
只有倍增和Tarjan两种算法可以跑LCA?
4.树链剖分
*声明:如果你不会树链剖分你可以不看这一块。
树上倍增嫌慢?Tarjan嫌内存太大操作太麻烦?树链剖分求LCA,你值得拥有!类似于树上倍增的思想,只不过加快了往上跳的速度而已。树链剖分的方法是,一条链子一条链子地往上跳!当跳到两个点所在的链子为同一条时,浅的那个点就是LCA。
xxxxxxxxxx
#include
#include
#define maxn 500010
#define maxm 500010
struct graph{ struct edge{ int to, next;
edge(){} edge(const int &_to, const int &_next){ to = _to;
next = _next;
}
}e[maxm << 1];
int head[maxn], k;
inline void init(){ memset(head, -1, sizeof head);
k = 0;
}
inline void add(const int &u, const int &v){ e[k] = edge(v, head[u]);
head[u] = k++;
}
}g;
int fa[maxn], son[maxn], size[maxn], dep[maxn];
int dfn[maxn], id[maxn], top[maxn], cnt[maxn], tot;
int n, m, s;
inline void swap(int &x, int &y){ int t = x; x = y; y = t;}
inline void dfs_getson(int u){ size[u] = 1;
for(int i = g.head[u]; ~i; i = g.e[i].next){ int v = g.e[i].to;
if(v == fa[u]) continue;
dep[v] = dep[u] + 1;
fa[v] = u;
dfs_getson(v);
size[u] += size[v];
if(size[v] > size[son[u]]) son[u] = v;
}
}
inline void dfs_rewrite(int u, int tp){ top[u] = tp;
dfn[u] = ++tot;
id[tot] = u;
if(son[u]) dfs_rewrite(son[u], tp);
for(int i = g.head[u]; ~i; i = g.e[i].next){ int v = g.e[i].to;
if(v != son[u] && v != fa[u]) dfs_rewrite(v, v);
}
cnt[u] = tot;
}
inline int lca(int u, int v){ while(top[u] != top[v]){ if(dep[top[u]] > dep[top[v]]) swap(u, v);
v = fa[top[v]];
}
if(dep[u] > dep[v]) swap(u, v);
return u;
}
int main(){ g.init();
scanf("%d%d%d", &n, &m, &s); for(int i = 1; i < n; i++){ int u, v;
scanf("%d%d", &u, &v); g.add(u, v);
g.add(v, u);
}
dfs_getson(s);
dfs_rewrite(s, s);
for(int i = 1; i <= n; i++){ int u, v;
scanf("%d%d", &u, &v); printf("%d\n", lca(u, v)); }
return 0;
}